MAT2705 24F homework and daily class log

Jump to current date!
[where @ is
located]
Daily lecture notes and your homework will appear here each day as it is assigned, including some PDF
and/or Maple problem solution files or PDF notes, with occasional links to
some MAPLE worksheets when helpful to illustrate some points where technology can be
useful. [There are 56 class days in the semester, 4
each normal week, numbered consecutively below and labeled
by the (first initial of the) day of the week.]
It is
important that you read the section in the book from which homework problems
have been selected before attempting them.
It is your responsibility to check homework here since most but not all homework
exercises are online in the MyLab Math portal entered through BlackBoard. Homework hints
and some textbook exercise solutions are also found here. You are
responsible for requesting any paper handouts or returned tests or quizzes from classes
you missed. Homework is understood to be done by the
next class meeting (unless that class is a test, in which case the
homework is due the following class meeting), but the online deadline will be
stated as midnight of the due day so that you have time in class or after to ask
questions that you did not submit via the Ask Your Instructor
online tool. You may correct submitted homework after the deadline without
having to request an extension. You have unlimited tries.
[[A
few occasional
homework
problems surrounded by double square brackets
[[...]] are not in the online homework
system but are important to do or at least read.]]
Read:
HOMEWORK ADVICE;
-
M: (August 26)
DURING CLASS:
Lecture
Notes 1.1a: Differential Equations: how to state them and "check" a solution;
<< READ THIS PLEASE!
summary handout: odecheck.pdf
<<< this is all you need to do the HW but please
read section 1.1 of the textbook, summarized in my
four pages of lecture notes linked above.
We will enter together the e-text MyLab Math portal
and homework software inside the Content page of
BlackBoard (Pearson materials) , as explained in the
welcome email message! Please be ready
for this by having connected your BlackBoard course
to the e-portal, creating a Pearson account in the
process.
New to Maple 3 minute video [also in opening screen of Maple]
AFTER CLASS (THIS IS THE HOMEWORK):
1) Log in to My Nova, choose the Class Schedule with Photos,
view fellow students.
2) Go to
BlackBoard and look at the class portal and Grade book
for our course: you
will find all your Quiz, Test and Homework grades here during the
semester once there is something to post. Everything else we do apart from
accessing our e-portal will take place through our
course website.
3)
Make sure you have Maple 2024 on your local
computer, available by
clicking here if you haven't already done so, and install it on your laptop when you get a
chance (it takes about 15 minutes or less total), If
you have any trouble, email me with an explanation of the errors. You are expected to be able to use Maple on your laptop when
needed. We will develop the experience as we go.
If
you have any trouble, email me with a copy of your worksheet and an explanation of the errors.
I can also help you in person.
You are expected to be able to use Maple on your laptop when
needed. We will develop the
experience as we go.
No
previous experience is assumed.
4) Enter the e-text MyLab Math
Pearson portal
if you have not already done so, as explained in the
welcome email message!
5)
Homework Problems:
1.1: 3, 5,
13, 33
(only a few problems so you can check out our class website and read about the
course rules, advice, bob FAQ, etc, respond with your email).
6) By the end of the week, reply to my
welcome e-mail from your OFFICIAL
Villanova e-mail account (which identifies you with your full name),
telling about your last math courses, your comfort level with graphing
calculators and computers and math itself, how much
experience you have with Maple if any (and Mathcad if appropriate) so far, why you chose your major, etc,
anything you want to let me know about yourself that will give me more of an
idea about you as a person. [For example, I like to do
humorous sketching.
and cooking.] Tell me
what your previous math course was named (if at VU: Mat1500 = Calc 1, Mat1505 = Calc
2, Mat2500 = Calc3).
[In ALL email to me, try to include the string "mat2705" somewhere in the
subject heading if you want me to read it quickly. I filter my email.]
-
T:
check info on sign up sheet;
dorm abbreviations;
Lecture
Notes 1.1b: Differential Equations: initial conditions
[extra:
initial data: what's the deal?];
[gravity
fall example]
1:1: 8, 23 [see
Maple plot (execute worksheets by clicking on the !!! icon on the
toolbar when necessary)];
formulating DEs: 27,
31 [as in 29 below: make a generic diagram like
this one to calculate the slope of the
tangent line and set it equal to the derivative
.mw; namely the change in y over the change in x between
these two points (x,y) and (y,-x)
equals dy/dx],
35, 43; perhaps in class together:
[[29.
Hint: recall perp lines have slopes which are negative
reciprocals, the normal line is perpendicular to the tangent line and passes
through the same point on the curve; make a diagram of the given point (0,1), a "generic" function graph curve
whose normal at a point (x,y) on the curve passes through
(0,1), and draw in the connecting normal line segment between these two
points and the perpendicular tangent
line, then compute the slope of the normal line from the two points, and then from the
negative reciprocal of the derivative value, finally equate the two
to get the DE: mw ]].
New Maple
users? I would be glad to show you one on one in my
office how to get started.
[memorize!: "A is proportional to
B" means "A = k B" where
k is some constant,
independent of A and B]
Proportionality statements
must be converted to equalities with a
constant of proportionality introduced:
y is
proportional to x: y ∝ x means y
= k x . [y is a multiple of x]
y is
inversely proportional to x: y ∝ 1/x
means y = k/x .
y is
inversely proportional to the square of x: y ∝ 1/x2
means y = k/x2
-
W: Math
Center video;
flyer;
Lecture
Notes 1.2: First order DEs independent of the unknown: y' = f(x)
[finding
particular antiderivatives interpreted as solving a
first order initial value problem illustrated by
textbook example problems:
lunar
landing example: mw, optional
ignorable: Swimmer
problem example: mw]
1.2: 1, 5, 15,
21 [Hint: write piecewise linear function from graph: v1(t) for first expression,
v2(t) for second expression, solve first IVP
for x1(0) = 0, second IVP for x2(4) = x1(4);
example: pdf,
mw],
25 (like lunar landing problem example above), 35,
together in class:
41 (first
solve bomb drop IVP, evaluate time when it arrives
at y = h (target height),
then solve projectile IVP with unknown inital velocity,
then impose that it reach height h at
the given time:
game plan; the second part is a
boundary value
problem!)
[[important
lesson on choice of units not in MyLab: 43, convert
final answer to appropriate units!]].
Send me the email about yourself with
your schedule attached please if you have not
already done so.
-
F: Quiz 1 on checking solutions to DEs, paper copy handed
out in class (read
Test/Quiz rules): due in
class Tuesday;
(see
archives for examplT
Lecture
Notes 1.3: First order DEs; Direction (= slope) fields and complications
[directionfields.mw] [ode1-complications]
1.3:
[use directionfields worksheet to plot:] 3, 5, [you don't need Maple to
choose here but it gives you some practice]
technicalities about
complications or not:
11,
15 [limited domain]; [partial
derivative with respect to y is just what you expect; differentiate
holding x fixed]
[[in
class plus HW drawing exercise: 1.3: 3:
hand draw in all the curves with a pencil on the slope field printout.
M: Labor Day

WEEK 2[-1]:
-
T:
Lecture Notes 1.4a: Separable first order DEs
[example
1: only implicit soln]
1.4 (separable DEs): 1,
4,
9 [use Maple for antiderivative! add
absolute value signs for ln integrals],
25, 27 [first expand
exponential into 2 factors e^(A+B)=e^A*e^B], 29.
-
W:
Lecture Notes 1.4b: Separable first order DEs
handout on
exponential behavior/ characteristic time [cooking
roast in oven remarks]
[how to choose
exponential plot window];
1.4: 33,
35,
41
[hint: first we need to evaluate the fraction of the total U + L which
is only U, namely U/(U+L)],
45 [attentuation of signal--characteristic length],
49 [cooling problem].
-
F: Quiz 2
(separable DEs and directionfields; see
archives):
together in
class:
1.4:
69 [hanging cable problem
[the
derivation of this DE just involves some simple trig and calculus, but
it is a complicated sequence of steps!this is typical of how you must follow
a derivation of a DE in a STEM application, not just be handed a DE to
solve;
hyperbolic functions are important in DEs! [see
wiki],
so is working with problems involving parameters];
catenaries in
engineering:
Google,
GoogleImage;
"fun" with Newton's law of cooling not online:
[65
CSI problem (same as the in lecture example and problem 49 but at
end we want to find a previous time instead of a subsequent time)].
Ask bob for the Maple solution worksheets when done.
WEEK 3[-1]:
- M: paper handout of classlist with dorms and phone
numbers;
check my office hours
in the class syllabus and your schedule
to see compatibility;
please read
quiz answer key;
Are online HW assignments available after
due date?
Lecture Notes 1.5a: Linear first order DEs
online handout: recipe for first order linear DE
1.5: 2, 5, 8, 21, 24 [u-sub integral];
(these involve using
rules of ln's and exp's).
For future reference to get Maple soln of a
DE (Maple template):
enter DE alone or DE plus initial conditions separated by commas,
from context menu at right
choose Solve DE, for
y(x)
> y ' = x y , y(0)=1
Use function notation to change independent variable:
> y '(t) = t y(t) , y(0)
= 1
If you use the d/dx y(x) from the
palette, you must use function notation y(x)
throughout the DE.
- T:
Lecture Notes 1.5b: Linear first order DEs:complications
[accumulation functions]
1.5: 15, 18, 24 (more practice);
27 (switching independent and dependent
variables),
30 ( just do the linear
procedure choosing the antiderivative as the definite integral from 1 to
x without evaluating it, choose integrating factor for x > 0
application to IVP).
- W: check grades
on BlackBoard please!
Lecture Notes 1.5c: Linear first order DEs:
Mixing Problems [1.5.37 worked
by hand]
[these mixing tank problems are an example of developing and solving a differential equation
that models a physical situation, and one where we have some intuition];
Solute (salt) plus solvent (water) makes a
solution (salt water!); concentration of
solute in solution = ratio of solute to solution;
different
concentrations equalize when mixed;
1.5: Use Eq. 18 in the book and plug in values of parameters:
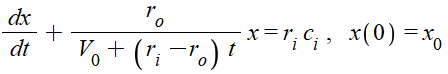
solve by hand, then
if necessary check with
Maple template;
respectively constant, decreasing, increasing volume cases:
33,
36,
37 (Maple worked solutions with textbook
exercise numbers).
Note: we are skipping 1.6: exact DE
etc. These are less important, and Maple can solve
these when needed anyway. A similar integrating factor technique works for
exact equations but
where the independent and dependent variables are on an equal footing.
-
F: Quiz 3 on linear DEs;
Chapter review problems are not in MyLab Math;
1.R
(review problems are not online!): in class we classify some of the odd problems
1-35 but don't solve them;
[[ solve 25 [it can be done in two ways by expanding out the square on the RHS
before integrating with integration constant C or by using a u-substitution
with integration constant K; express K in terms of C by
combining the two terms in the K solution [use the identity for expanding out (x+1)3
= x3+3 x2 +x+1] and then comparing with the C
solution];
both separable and linear:
solve 31 in two ways and compare
the results;
solve 35 in two ways and compare the results;
in both cases ---different
constants enter your expressions, show how they
agree]].
Catch up on
improving HW score.
WEEK 4[-1]:
Chapter 2 is just applications of chapter 1.
-
M:
Lecture Notes
2.1a: First order DEs: Logistic Equation
online
handout on solution of
logistic DEQ
[Maple: directionfield,
integral formula,
shape];
2.1 (only the logistic
DE part of the reading is necessary):
5 (resolve the DE this one time following the steps in the Lecture Notes/handout
or just use the final formula),
17 (see Maple worksheet for setup
problem 15);
21 (initial value of population and its derivative given
instead of population at two times, need to set k and P(0)
with two conditions),
23 (Rewrite
in form dx/dt = k M x - k x2
= k
x (M - x) to identify first k and then M
to then use the logistic
solution formula.).
- T:
Lecture Notes 2.1b: First order DEs: More models, Separable: f(y)
2.1 (other population models):
online handout on
DE's that don't involve the ind
var explicitly;
cubic
example;
11 ["inversely propto sqrt": use β =
k1/P^(1/2), δ =
k2/P^(1/2) in eq.(1),
beta and delta are fractional
(logarithmic derivative) birth/death rates;
this leads to P' ~ P^(1/2)]
13 [P' ~ P^2],
39 [oscillating growth,
plot pure exponential and solution together, see Maple worksheet];
optional: growth rate cutoff:
30,31 (not online).
-
W:
Lecture Notes 2.3: First order DEs: acceleration models
2.3 (acceleration-velocity models:
air resistance, section resistance
proportional to velocity only, omit example 3):
1, 3,
9 [remember weight is mg, so mg = 32000 lb determines
mass
m = 1000 in USA "slug" units, convert final speed to mph
for interpretation!],
19.
[optional reading
to show what is possible:
air
resistance in detail (example of a piecewise defined DE and solution and
the importance of dimensionless variables;
comparison of
linear, quadratic cases; numerical
solution for
any power]
-
F: Quiz 4 on the logistic DE; quiz 3 answer key online;
Lecture Notes 2.4: First order DEs: numerical DE solving
with Euler's method
[Euler
Tutor template for HW]
2.4:
1, 7
WEEK
5[-1]:
- M: Lecture Notes 3.1: linear systems of equations: elimination, DEs;
[mw]
[inconsistent 3x3 system];
Read 3.1 on linear systems (review of high school topic solving 2 or 3 linear equations in
2 or 3 variables),
3.1: 2x2: 3, 5, 7; 3x3: 9; 2x2 IVP: 23, 27.
- T: Test 1 on first order DEs: one mathematical
problem of each type, no word problems;
-
W: 3.2:
Lecture Notes 3.2: matrices and row reduction "elimination";
handout on
RREF (Reduced Row Echelon Form, section 3.3)
[see bob's examples 2,
3 using Maple];
3.2: 1, 5, 7, 9 [these are partially reduced, only requiring successive
backsubstitution to solve, you can do this on paper];
11,13,15,
[you may do these by hand on
paper or use step-by-step row ops with the MAPLE Tutor; we ALWAYS want a
complete reduction, you can insert the complete Gauss-Jordan reduced row
echelon form (RREF) to get practice] ;
you must learn a technology method since this is insane to do
by hand after the first few simple examples;
23 [matrix with a parameter, reduction
depends on value];
in class
we reduce two matrices in this Maple file
using the LinearSolveTutor.
-
F: No Quiz;
we catch up with RREF details, no
partial reductions as in 3.2!;
Lecture Notes 3.3: Row reduction solution of linear systems;
online handout on
solving linear systems example
[.mw];
we always want to do a full [Gauss-Jordan] reduction, not the partial Gauss
elimination reduction also described by the textbook;
in class practice worksheet;
3.3:
reduce: 3, 9, 14, 17, 19,
solve: 21, 23, 29
You can use
this template to invoke the
Gauss-Jordan EliminationTutor for the homework problems.
WEEK 6[-1]:
-
M:
Check BlackBoard grades against your papers;
Lecture Notes 3.3: Balancing Chemical Reaction Application
[online chem balancer]
(application of integer matrices in homogeneous linear systems)
[lecture solutions]
homework for fun [plus explanation of mixed chemical reactions!][soln]
-
T:
Lecture Notes 3.4: Matrix operations
3.4: 1, 5, 9, 2, 11, 13, 15, 17, 19.
[matrix multiplication:
summary handout,
Maple]
- W: Lecture Notes 3.5:
square matrix inverses;
[2x2 example]
3.5: 1, 5, 7, 9 (use the 2x2 inverse formula to do by hand for
practice);
11, 19 (row reduce augmented matrix, then check with
Maple inverse);
23 (multiply both sides by inverse matrix to solve; Maple
check).
Memorize for frequent use:
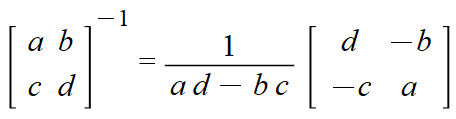 .
.
Switch
diagonal entries. Change sign off-diagonal entries. Divide by determinant.
Always check inverse in Maple if you are not good at remembering this.
-
F: Quiz 5;
Lecture Notes 3.6: Matrix determinants; [examples]
[forget minors, cofactors,
forget Cramer's rule (except remember what it is when old-fashioned texts
refer to it), use Maple to evaluate determinants; we only need row
reduction evaluation to understand determinants];
3.6:
use a few SwapRow, AddRow ops with the G-J reduction Tutor to find upper
triangular form for a few, or just use Maple (Standard Operations) to
evaluate the determinant:
7 (easy! AddRow leads to zero row, zero value),
9, 10, 13,
29 (Cramer's rule just to be aware);
catch up on old
HW.
WEEK 7[-1]:
- M:
Lecture Notes
4.1: R^2 and R^3: Linear independence;
R^n spaces and linear
independence of a set of vectors [vector
space rules];
now we look at linear system coefficient matrices
A as collections of columns A = < C1| ... |Cn >,
matrix multiplication on the right by a column of
coefficients as taking linear combinations of those columns,
A x = x1 C1 + ... + xn Cn
and solving homogeneous linear systems of equations A x = 0 as
looking for linear relationships among those columns (nonzero solns=linear
rels) ;
4.1: 5, 7; 13; 15, 17; 19, 23; 29, 31, 33 [example].
-
T:
Lecture Notes
4.2: Vector spaces and subspaces [in
class exercise];
(homogenous linear systems define
subspaces!);
[note only a set of vectors x resulting from the solution of a linear homogeneous condition
A x = 0 can be a subspace of a vector
space; interpretation: lines, planes, ..., hyperplanes through the origin];
4.2: 1, 3, 7, 11; 15, 21.
- W:
Lecture Notes 4.3: Span of a set of vectors
>
extended exercise from
yesterday(pick up on page 3);
so far: linear
independence (A x = 0),
or express a vector as a linear combination of other vectors (A x =
b) ;
now give the name span to the subspace of all linear combinations of a set of
vectors, like we get from solving A x = 0;
to solve A x =
b is express b as a linear combination of the
columns of A if b lies in the
span of those columns;
BUT the solution space itself is in the space
of coefficients, and the row reduction mechanism automatically provides a
unique linear combination expression for each set of coefficients whose
linear combination results in the zero vector: the span of the "basic"
coefficient vectors in the solution representation is the solution
"subspace".
4.3: 1, 3, 5, 7; 9, 13; 17, 21.
Teach-in on Lebanon crisis 5-6pm, free dinner at 6pm

-
F: No Quiz 6;
Lecture Notes 4.4:
Bases;
[handout: new coordinate grids] [pick
your own basis] [subspaces?]
4.4: 1, 3, 5 [zero row!], 7;
9 [this is in already reduced form, find solution as in class example, pull apart to find coefficient vectors of
parameters, repeat for next 4 problems reducing first in the last 3],
13 [equations already in reduced form! express all 4 variables in terms of
free variables c, d, read off coefficients of those two free variables];
15, 17 [use technology for all row reductions].
Fall break 

WEEK 8[-1]:
-
M: 4.7 Lecture Notes 4.7:
Vector spaces of functions;
bridge to vector spaces
whose elements are functions.
Part 2 of course begins: transition back to DEs:
read the 4.7 subsection
on "Function Spaces" and then examples 3, 4, 6, 7, 8;
[if you are curious, example 5 illustrates the partial fraction decomposition
needed in engineering integration but Maple does this easily];
Optional worksheet explaining the
vector space of (at most) quadratic functions [quadratics.mw];
4.7: 9, 11 [is the condition on the coefficients a linear homogeneous
condition? only if so do these form a subspace]
14 [note that any two
(nonzero!) functions of x that are not proportional with a constant
ratio are automatically linearly independent],
15 [Hint: solve c1(1 + x) + c2(1 - x) + c3(1 - x2) = 0, for unknowns c1,c2,c3;
are there nonzero solutions? if not, these are linearly independent polynomials, in terms of which any quadratic
expression in x can be written],
18 [are the two functions proportional? if not, they are linearly
independent].
new coordinates on
the plane workshop. Complete for HW if not finished in class.
Read
why we are doing this here.
Monday exercise on grids completed here.
- T:
Lecture Notes
5.1a:
2nd order linear DEs: an intro;
read 5.1 up to the subsection on
Linear Independent Solutions (this is a long section);
Memorize: y ' = k y < -- > y = C e k x (from
chapter 1)
y '' + ω2 y = 0 < -- > y =
C1 cos(ω x) + C2 sin(ω x)
[when x is a time variable, "omega" = ω is the angular frequency "radians per time unit"
]
5.1: 1, 3, 9, 11 [verify solutions, then impose initial conditions];
17 [nonlinear DE does not allow scaling of solutions]
- W: Lecture Notes
5.1b:
constant coefficient 2nd order linear homogeneous DEs;
repeated root plot
[problem 49 worked here is useful for working with exponentials];
5.1[after Linear Independent Solutions subsection]: 33, 35, 38, 39.
[We will talk about the Wronskian matrix next time.]
- F: Quiz 6; no office hour today (dept meeting);
Lecture Notes
5.2:
The Wronskian and higher order constant coefficient 2nd order linear DEs;
ignorable extras: [Maple Wronskian][example
1]
5.2: 1 [set a linear combination equal to zero, then gather
coefficients of powers of x, set equal to zero to solve for the unknown
coefficients],
7,
13, 17,
23 [the particular soln
is a constant function so inserting an unknown constant into the LHS gives
correct value].
WEEK 9[-1]:
- M:
Lecture Notes
5.3.0: Complex arithmetic and complex exponentials
handout on complex
arithmetic, exponentials
[if interested: Maple
commands; the complex number i =
sqrt(-1) is
uppercase I in Maple];
no homework.
- T: Test 2 on chapters 3, 4.
[check out 22S T2]
- W:
Lecture Notes
5.3a:
higher order constant coefficient linear homogeneous DEs and complex
exponentials: distinct roots;
(use Maple to find
roots of characteristic equation).
5.3: 1, 9,
17, 23, 33.
Th: Halloween!
- F:
no quiz during test week;
Lecture Notes
5.3b:
higher order constant coefficient linear homogeneous DEs: repeated roots;
5.3: 5, 11, 13, 19, 25, 35 [ignore instructions to
use one solution to find more; just find roots with Maple!]
WEEK 10[-1]:
- M: Lecture Notes 5.3c: sinusoidal
and decaying sinusoidal functions;
To plot envelope
functions of decaying amplitude together with the decaying oscillation, do:
> plot( [A e -k x, -A e -k x, e -k x
(
c1 cos(ω x) + c2 sin(ω x)
)], x=0..10)
where <c1,c2>
= <A cos(δ), A sin(δ)>
transforms
Cartesian to polar coordinates in the parameter plane (draw a diagram).
For HW try this with y = e -x/2
(-3 cos(10 x) +5 sin(10 x) )
.
Examples.
- T: Test 2 back in class; see
answer key;
Lecture Notes
5.4: Linear homogeneous 2nd order DEQ with constant positive coefficients (damped harmonic oscillators);
5.4: read worksheet for help on this
problem:
3: Undamped oscillator: y '' + ω2 y = 0 < -- > y =
C1 cos(ω x) + C2 sin(ω x)
[omega is a small integer for this problem]
frequency vocabulary: when x is a time variable, "omega" = ω is the angular frequency "radians per time unit" as opposed to
just "frequency" f =
ω/(2π ) or "revolutions or cycles per time unit" as in physics, but in our class we
will just say "frequency" for ω, assumed to be expressed in radians per time
unit or converted to revolutions per time unit as convenient;
see also
damped
harmonic oscillators and
RLC circuits, and
Hertz
(computers now have
GHz clock speeds),
"cycles per second"];
13
(goal: maximum positive displacement setting derivative to zero);
solve these next problems by hand, determine phase-shifted form, then plot
undamped and damped solutions together:
15 overdamped,
17 critically damped,
19
underdamped.
Here are the
textbook parameter exercises solved so you can edit the plots to help
pick out the online plot choice after solving these problems by hand.
The evaluation of the numerical phase shifts is also explained for each
problem. [In fact the signs of the initial data are actually enough
to distinguish which plot is correct.]
- W:
Lecture Notes
5.5: NON-homogeneous 2nd order DEQ with constant coefficients
summary handout on driven
(nonhomogeneous) constant coeff linear DEs;
[final exercise on this
handout sheet: pdf
solution];
5.5: 1, 3, 8
[just express cosh or sinh in terms of exponentials],
10, 33,
35;
[not many of the book RHS driving
functions are physically interesting here;
we will not cover "variation of parameters"; the book
presentation of the method of undetermined coefficients is a recipe with
little justification (educated guess), instead the undetermined coefficient
method handout shows exactly how and why one gets
the particular solutions up to these coefficients].
- F: Quiz 7 on underdamped harmonic oscillator;
Lecture Notes
5.6a: Driven damped harmonic oscillators;
[today
example with resonance
calculation side by side; .mw],
5.6:
11 [ HW portal wants phase-shifted
cosine form for both steady state and transient sinusoidal factor, phase
shift between 0 and 2 Pi, decimal solutions, then plot],
13 [the exact
numbers are ridiculous, just use the Maple solution and find the
phase-shifted cosine form of the transient and steady state solutions to 3
decimal places, see the previous Maple worksheet final section].
No
afternoon Office Hour.
Mendel Medal talk 2pm Mullen Center. Be there (early to get a seat).
Speakers are usually really good.
WEEK 11[-1]:
- M: recap of last time:
resonance plots;
Lecture Notes
5.6b: Driven damped harmonic oscillators: special cases;
summary
handout on damped harmonic oscillator driven by sinusoidal driving function
[1 sheet printable version];
[only for fun:
beating!]
5.6: 1, 3 [ undamped solutions driving frequency not equal to natural
frequency],
17 [resonance calculation with reasonable numbers; but don't
"rationalize" sqrt in denominator! will be marked wrong].
- T: 6.1:
Lecture Notes 6.0 Eigenvectors
and eigenvalues of 2x2 matrices;
Lecture Notes
6.1a: Eigenvectors and eigenvalues (last page tomorrow 3x3
example);
bob uses the Maple worksheet
EigenExploreDrag2.mw to
graphically determine the eigenvectors and eigenvalues of some 2x2 matrices.
[in the lecture bob first explains why we want to do this
with a motivating example of a
coupled system of DEQs and its
directionfield]
6.1: 1, 2, 7.
- W:
Lecture Notes
6.1b: Eigenvectors and eigenvalues: n>2 and more (linear independence,
complex eigenvectors:
examples);
6.1: 15, 19, 23 (upper triangular so diagonal values are eigenvalues!),
31 (complex eigenvalues)
[do everything by hand for 2x2 matrices;
For 3x3 or higher, go thru process: use Maple determinant: |A-λI|
= 0 (right click on matrix, Standard Operations), then solve to find characteristic equation and
its solutions, the eigenvalues,
back sub them into the matrix equations (A-λI)
x = 0 and solve by rref, backsub, read off eigenvector basis of
soln space, NO POLYNOMIAL DIVISION! compare to Maple's Eigenvector result,
from the context sensitive menu].
Ignore
polynomial division discussion (as useless as long division!), use technology for roots of polynomials
and determinants!
- F:
Quiz 8 on finding resonant frequency for underdamped harmonic oscillator of
previous quiz.
Lecture Notes
6.2: Diagonalization [short
version in class];
summary: diagonalization;
[diagonalize: 3x3 examples];
6.2: 3, 10, 13, 19, 25 [use Maple for det and
solve for eigenvalues, then by hand find eigenvectors, use Maple for matrix
multiplication; check with Eigenvalues etc; online
eigenvector matrices are all integer valued, so perhaps it is worth scaling
up your eigenvectors to integer values].
in class
this handout exercise:
For the matrix: A = <<1|4>,<2|3>> entered by rows,
use Maple to find the eigenvalues and the basis changing matrix
B = <b1|b2> of corresponding eigenvectors, evaluate the
matrix product AB = B-1A B to see that it is
diagonal and has the corresponding eigenvalues in order along the diagonal,
and use the coordinate transformations
x = B y and y = B-1
x to find the new coordinates of the point
x = <x1, x2> =
<-2,4> in the plane. Then make a grid diagram with the new (labeled)
coordinate axes associated with this eigenbasis
(labeled also by the eigenvalue λ =
<value> ) together with basis vectors
and the projection parallelogram of this point.
Support your fellow
students in the Villanova Student Musical Theatre performance of
Footloose! They are
doing a great job and there are
plenty of seats left!
NO office hour
today, dept meeting!
WEEK 12[-1]:
- M:
Lecture Notes
7.3a: 1st order linear homogeneous DE systems: real
eigenvalues:
(notes are a summary of what we already done with a
concrete 2x2 example);
just use Maple to get eigenvalues and eigenvectors, form linear combination
of eigenvalue exponentials and eigenvectors to get general soln; remember
to enter arbitrary constants with subscripts c1 ...
7.3:2x2 with direction field
5
(but no need to plot, use slopes of eigenlines and signs of eigenvalues for
arrow directions along eigenlines as explained in this Maple worksheet);
3x3:
17.
- T: 7.3
Lecture Notes
7.3b: 1st order linear homogeneous DE systems:
complex
eigenvalues:
[short version
in class]
[new shortest
version; maple]
7.3:
15 [no need to
plot, check directionfield arrow A x direction along positive vertical axis
say at x1=0, x2 = 1],
25.
No office hour after
class.
- W: HW catch up, ask help from bob; Review questions?
Questions about past test 3's. See
archive; check out the quiz 8
answer key there;
we will do 22S problem 3 in class to have more
practice with complex eigenvalues.
- F: Take Home test out, start in class. Due Wednesday
after T-day break.
3 problems: problem 1 combines quizzes 7 and 8 while
problems 2
and 3 are 3x3 linear DE systems with respectively complex (22S) and real
(23S)
eigenvalues (see
archive) [MERCY: PROBLEM 3
DELETED]
please read the test rules.
WEEK 13[+1]:
- M:
Lecture Notes
7.3d: mixing tanks, etc; [multicompartimental
models
eqns];
[open flow thru system with real eigenvalues, closed system
example 4
flow thru system with complex eigenvalues];
7.3:
33 (open, real,
unassigned),
37 (closed,
complex USE AS TEMPLATE, you might need "evalc" on your eigenvector
matrix to convert to Re plu Im parts);
use eigenvalues and eigenvectors from Maple, write down linear
combination of eigenvalue exponentials times eigenvectors as general soln
(plus Re,Im aparts with complex case), then impose initial conditions.
QUICK. no need to plot, just pick out the plot with the correct asymptotes
for the 3 variables.
- T: work on Test 3 in class. Be safe traveling!
T-Day break 
-
M:
work on test 3 in class.
- T: last topic: undamped coupled harmonic oscillator systems: undriven
case:
Lecture Notes
7.5a: mass spring systems;
[figure8curve.mw,
periodic:
lissajous figures!,
aperiodic:
2mass2spring-aperiodic.mw];
7.5: 3, 5 [Maple quick check template:
epc4-7-5-template.mw]
you just have to identify the natural frequencies ωi =
sqrt(-λi ) of the accordian
(opposite sign component eigenvectors) and tandem (opposite sign
component eigenvectors) modes.
-
W:
Test 3 due, unless extenuating circumstances: email for extention till
Friday;
undamped coupled harmonic oscillator systems: driven case, given
frequency;
Lecture Notes
7.5b: driven mass spring systems (pages 3-4);
[again figure8curve.mw];
result for the system in the previous class exercise driven
by a specific frequency oscillating force :
2mass2spring-short-driven.mw;
(this is the last final exam topic,
stopping short of the resonance calculation with general frequency):
use the template epc4-7-5-template.mw
to evaluate the matrix and eigenstuff,
7.5:
9
[driven case, need initial conditions, final exam problem, check archive];
for the last two problems,
only eigenvalues and eigenvectors necessary to identify eigenfrequencies and
amplitude ratios/signs, but the particular solution via the method of
undetermined coefficients is needed to identify the response vector
amplitute ratios and relative signs:
11 (driven
case, initial
conditions irrelevant, only eigenvalues and eigenvectors needed),
13 (undriven case, 3x3 matrix, no
initial conditions, only eigenvalues and eigenvectors needed)
no online
problems exploring rseonance...or damping... but bob will show you what this
looks like anyway.
- F: undamped couple harmonic oscillator systems: resonance;
Lecture Notes
7.5b: driven mass spring systems
(pages 1,2,5 today)
[again figure8curve.mw]
no homework, topic not on final exam; catch up on online HW not already 100
percent assignments.
WEEK 14 [-1]:
-
M:
in class shortened previous final exam practice exercise:
27523s4-24f.pdf.
-
T[F]:
damping and resonance:
damped coupled harmonic oscillator
systems?
[again figure8curve.mw];
dynamic damping video (for fun, 9.5 minutes, dynamic damping, plus
another 8 minutes);
earthquake
analysis.
-
@ W:
CATS evaluation at beginning of class;
Watch the 4 minute Google linked video of resonance NOT!
(but see the
engineering explanation linked PDF for the detailed explanation):
Tacoma Narrows Bridge collapse:
Wikipedia;
Google (You-Tube video)]
(4 minutes);
a real resonance bridge problem occurred more
recently: the Millenium Bridge
resonance (5 minutes).
.
FINAL EXAM:
(not cumulative)
2705-06 MWF/T 11:45: Tues, Dec 17 8:30 am - 11:00 am
2705-07 MWF/T
12:50: Fri, Dec 20 2:30 pm - 5:00 pm
[switch okay with permission]
Homework assignment
catch up possible till end of exam period,
notify me if you are still
working at it towards the end of exam period.
MAPLE and G.Calc. CHECKING ALLOWED FOR QUIZZES, EXAMS
16-jun-2024 [course
homepage]
[log from last time taught]



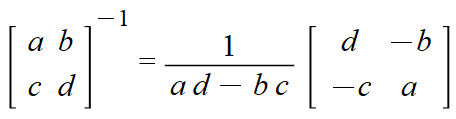 .
.



