:
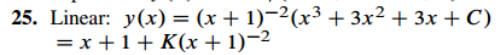
EPC4 Chapter 1. Review Problems 1-35 [We will just look at the odd problems.]
Classify (but don't solve) each DE as
Some may be both separable and linear in y.
For in class work, here is a scan of the HW page:
single column list [page scan: epc4-1-R.pdf];
problems 31-36 are more than one type and the instructions are to solve in
the two different ways and compare.
25
can be done in two ways by expanding out the square on the RHS
before integrating with integration constant C or by using a u-substitution
with integration constant K; express K in terms of C as given in the book supplied answers by
combining the two terms in the K solution [identity for expanding out (x+1)3 !] and then comparing with the C
solution];
Binomial identity for problem 25 (try it in Maple) needed for two ways of
integrating:
> expand ( (x+1)3 )
x3+3 x2+3 x+1
Back of book answer:
:
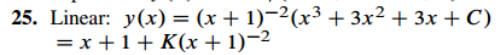
Express K in terms of C. The point is that different ways
of solving the DE or even different antiderivative expressions can make the
final result look very different. [ Use identity to replace first 3 terms in the
parentheses on the top line, then expand the expression and compare with the
second line.]
Namely:
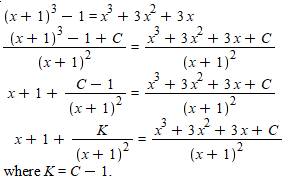
Similarly do these in two ways and compare constants of integration.

