Edwards Penny Calvis:
Differential Equations and Linear Algebra
selected homework problems: Maple worksheets

These are worked problems from a few textbook examples and the exercises in this textbook, mostly using the hard numbers of the textbook stated problems, but some occasionally use the random parameters of the online homework system MyLab Math.These are extracted from the class homework log
  https://www34.homepage.villanova.edu/robert.jantzen/courses/mat2705/homework.htm
and were created by Robert Jantzen at Villanova University, now retired. Ignore the lecture notes linked to the section titles.

These are extracted from the homework log: https://www34.homepage.villanova.edu/robert.jantzen/courses/mat2705/homework.htm
from the website of Bob Jantzen at Villanova University Dept of Math and Stat.

Execute worksheets by clicking on the !!! icon on the toolbar when necessary.

• Chapter 1: First order differential equations
• Chapter 2: Mathematical Models and Numerical Methods
• Chapter 3; Linear Systems and Matrices
• Chapter 4: Vector spaces
• Chapter 5: Linear equations of higher order
• Chapter 6: Eigenvalues and Eigenvectors
• Chapter 7: Linear Systems of Differential Equations
• Chapter 8: Driven Linear Systems of Differential Equations

Chapter 1: First order differential equations

• 1.1: Differential Equations: initial conditions
  [gravity fall example]
  23, 27, 29.
  
• 1.2: First order DEs independent of the unknown: y' = f(x)
  Exanple 2, Example 4
  21, 41, 43.
  
• 1.3: First order DEs; Direction (= slope) fields and complications
  [directionfields.mw] [ode1-complications]
  3,  15.
  
  
• 1.4: Separable first order DEs
  Example 1,
   9, 27.
  
• 1.4: Separable first order DEs
  Example 5
  [how to choose exponential plot window];
  1.4: 33, 35,
  41 [hint: first we need to evaluate the fraction of the total U + L which is only U, namely U/(U+L)],
  45 [attentuation of signal--characteristic length],
  49 [cooling problem].
  
• 1.4: Separable first order DEs
  65, 69 [hanging cable problem: derivation of this DE just involves some simple trig and calculus, but it is a complicated sequence of steps!this is typical of how you must follow a derivation of a DE in a STEM application, not just be handed a DE to solve].
  
  
• 1.5: Linear first order DEs
  For future reference to get Maple soln of a DE (Maple template):
  enter DE alone or DE plus initial conditions separated by commas, from context menu at right choose Solve DE, for y(x)
  > y ' = x y , y(0)=1
  Use function notation to change independent variable:
  > y '(t) = t y(t) , y(0) = 1
  If you use the d/dx y(x) from the palette, you  must use function notation y(x) throughout the DE.
  
  
• 1.5: Linear first order DEs 
  [accumulation functions]
  30.
  
• 1.5: Linear first order DEs: Mixing Problems [1.5.37 worked by hand]
  [these mixing tank problems are an example of developing and solving a differential equation that models a physical situation, and one where we have some intuition];
  Solute (salt) plus solvent (water) makes a solution (salt water!); concentration of solute in solution = ratio of solute to solution;
  different concentrations equalize when mixed;
  1.5:  Use Eq. 18 in the book and plug in values of parameters:
   
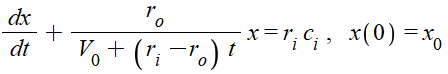
  solve by hand, then if necessary check with Maple template;
  respectively constant, decreasing, increasing volume cases: 33, 36, 37 (Maple worked solutions with textbook exercise numbers).
  
  

Chapter 2: Mathematical Models and Numerical Methods

• 2.1: First order DEs: Logistic Equation
  [Maple: directionfield,  integral formula, shape];
  17, 21, 23.
  
• 2.1: First order DEs: More models, Separable: f(y)
  2.1 (other population models):
  DE's that don't involve the ind var explicitly:  cubic example,
  39,  30,31,
  
  
• 2.3: First order DEs: acceleration models
  acceleration-velocity models: air resistance,
  1, 3, 9.
  air resistance: comparison of linear, quadratic cases; numerical solution for any power.
  
  
•  2.4: First order DEs: numerical DE solving with Euler's method
  Euler Tutor template
  
  

Chapter 3: Linear Systems and Matrices

• 3.1: linear systems of equations: elimination, DEs; [mw]
  15 inconsistent 3x3 system,
  
• 3.2: matrices and row reduction "elimination";
   examples 2, 3.
  
  
• 3.3: Row reduction solution of linear systems;  [.mw];
  template for the Gauss-Jordan EliminationTutor for the homework problems.
  
  
• 3.3: Balancing Chemical Reaction Application  [online chem balancer]
  (application of integer matrices in homogeneous linear systems) [lecture solutions]
  homework for fun [plus explanation of mixed chemical reactions!][soln]
  
  
• 3.4: Matrix operations
  Maple.
  
• 3.5: square matrix inverses; [2x2 example]
   23.
  
  
• 3.6: Matrix determinants; [examples]
  
  

Chapter 4: Vector spaces

• 4.1: R^2 and R^3: Linear independence;
  example.
  
• 4.2: Vector spaces and subspaces [in class exercise]
  
• W: Lecture Notes 4.3: Span of a set of vectors > extended exercise from previous day
  so far: linear independence (A x = 0), or express a vector as a linear combination of other vectors (A x = b) ;
  now give the name span to the subspace of all linear combinations of a set of vectors, like we get from solving A x = 0;
  to solve A x = b is express b as a linear combination of the columns of A if b lies in the span of those columns;
    9.
  
  
•  4.4: Bases; [handout: new coordinate grids] [pick your own basis] [subspaces?]
  
• 4.7: Vector spaces of functions
  bridge to vector spaces whose elements are functions.
  
  Part 2 of course begins: transition back to DEs:
  Optional worksheet explaining the vector space of (at most) quadratic functions: quadratics.mw;
  new coordinates on the plane workshop.
  Read why we are doing this here.
  exercise on grids completed here.
  
  

Chapter 5: Linear equations of higher order

•  5.1a: 2nd order linear DEs: an intro;
  Memorize: y ' = k y  < -- > y = C e ^{k x} (from chapter 1)
    y '' + ω² y  = 0 < -- >  y = C₁ cos(ω x) + C₂ sin(ω x)
  [when x is a time variable, "omega" = ω is the angular frequency "radians per time unit" ]
  
  
• 5.1b: constant coefficient 2nd order linear homogeneous DEs;
   repeated root plot [problem 49 worked here is useful for working with exponentials];
  
  
•  5.2: The Wronskian and higher order constant coefficient 2nd order linear DEs;
  ignorable extras: [Maple Wronskian][example 1]
  23.
  
  
•  5.3.0: Complex arithmetic and complex exponentials
  Maple commands; the complex number i = sqrt(-1) is uppercase I  in Maple,
  
  
•  5.3a: higher order constant coefficient linear homogeneous DEs and complex exponentials: distinct roots;
   (use Maple to find roots of characteristic equation).
  17.
  
  
• 5.3b: higher order constant coefficient linear homogeneous DEs: repeated roots;
  
  
•  5.3c: sinusoidal and decaying sinusoidal functions;
  To plot envelope functions of decaying amplitude together with the decaying oscillation, do:
  > plot( [A e ^{-k x}, -A e ^{-k x}, e ^{-k x} ( c₁ cos(ω x) + c₂ sin(ω x) )], x=0..10)
  where <c₁,c₂> = <A cos(δ), A sin(δ)>
  transforms Cartesian to polar coordinates in the parameter plane (draw a diagram).
  For HW try this with y =  e ^-x/2 (-3 cos(10 x) +5 sin(10 x) ) .
  5.4.1.
  
• 5.4: Linear homogeneous 2nd order DEQ with constant positive coefficients (damped harmonic oscillators);
  3: Undamped oscillator:  y '' + ω² y  = 0 < -- >  y = C₁ cos(ω x) + C₂ sin(ω x) [omega is a small integer for this problem]
  frequency vocabulary: when x is a time variable, "omega" = ω is the angular frequency "radians per time unit" as opposed to just "frequency" f = ω/(2π ) or "revolutions or cycles per time unit" as in physics, but in our class we will just say "frequency" for ω, assumed to be expressed in radians per time unit or converted to revolutions per time unit as convenient;
  see also damped harmonic oscillators and RLC circuits, and Hertz (computers now have GHz clock speeds),  "cycles per second"];
  13
  Here are the textbook parameter exercises solved so you can edit the plots to help pick out the online plot choice after solving these problems by hand. The evaluation of the numerical phase shifts is also explained for each problem. [In fact the signs of the initial data are actually enough to distinguish which plot is correct.]
  
• 5.5: NON-homogeneous 2nd order DEQ with constant coefficients
   3, 8, 10, 33, 35;
  
  
• 5.6a: Driven damped harmonic oscillators;
   [example, resonance plots]
  11.
  
•  Lecture Notes 5.6b: Driven damped harmonic oscillators: special cases;
  [beating!]
  17.
  

Chapter 6: Eigenvalues and Eigenvectors

• 6.0 Eigenvectors and eigenvalues of 2x2 matrices;
  6.1a: Eigenvectors and eigenvalues;
  bob uses the Maple worksheet EigenExploreDrag2.mw  to graphically determine the eigenvectors and eigenvalues of some 2x2 matrices.
  [in the lecture bob first explains why we want to do this with a motivating example of a coupled system of DEQs and its directionfield]
  
• 6.1b: Eigenvectors and eigenvalues: n>2 and more (linear independence, complex eigenvectors: examples);
  
  
• 6.2: Diagonalization [short version in class];
   [diagonalize: 3x3 examples];
  in class this handout exercise:
  For the matrix:  A = <<1|4>,<2|3>> entered by rows, use Maple to find the eigenvalues and the basis changing matrix B = <b1|b2> of corresponding eigenvectors, evaluate the matrix product A_B = B^-1A B to see that it is diagonal and has the corresponding eigenvalues in order along the diagonal, and use the coordinate transformations x = B y and y = B^-1 x to find the new coordinates of the point x = <x₁, x_2> = <-2,4> in the plane. Then make a grid diagram with the new (labeled) coordinate axes associated with this eigenbasis (labeled also by the eigenvalue λ = <value> ) together with basis vectors and the projection parallelogram of this point.
  

Chapter 7: Linear Systems of Differential Equations

• 7.3a: 1st order linear homogeneous DE systems: real eigenvalues:
  (concrete 2x2 example);
  5, 17.
  
  
• 7.3b: 1st order linear homogeneous DE systems: complex eigenvalues: [short version in class]
  [new shortest version; maple, maple2]
  15, 25.
  
• 7.3d: mixing tanks, etc; [multicompartimental models eqns];
  [Exanple 2: open flow thru system with real eigenvalues, 
   closed system Example 4 flow thru system with complex eigenvalues];
  33 (open, real),
  35,36 (open, real; closed, complex, example 2),
  37 (closed, complex).
  
• 7.5a: undriven mass spring systems;
  [figure8curve.mw, periodic:  aperiodic: 2mass2spring-aperiodic.mw];
  1-7template, 1-7solutions.
  
  
• 7.5b: driven mass spring systems [again figure8curve.mw];
  result for the system in the previous class exercise driven by a specific frequency oscillating force :
  2mass2spring-short-driven.mw;
  3_9, 11, 8-10,
  13 (undriven)
  14 (dynamic mass damper.
  
  
• 7.5b: driven mass spring systems
   [again figure8curve.mw]
  25-29 (2 axel auto)
  
  
• dynamic damping video (for fun, 9.5 minutes, dynamic damping, plus another 8 minutes);
  earthquake an (two axelalysis.
  
  
• Watch the 4 minute Google linked video of resonance NOT!
  (but see the engineering explanation linked PDF for the detailed explanation):
  Tacoma Narrows Bridge collapse: Wikipedia; Google (You-Tube video)] (4 minutes);
  a real resonance bridge problem occurred more recently: the Millenium Bridge resonance (5 minutes).

Chapter 8: Driven linear systems of differential equations

• 8.2: 1, 11, driven mixing tank
  
• 8.3: Example 2, Example 2-2nd order,