with Calc II and some trigonometry!
But Maple makes it come alive!
[National Museum of Math, NYC across the park from Eataly]
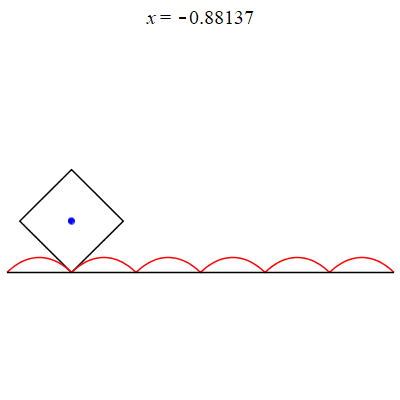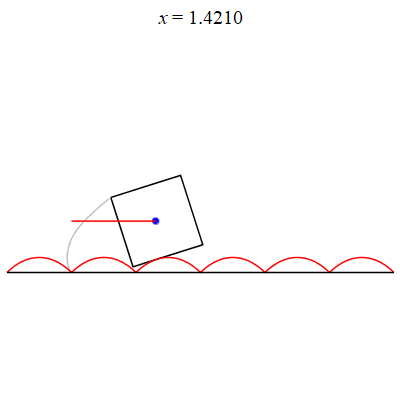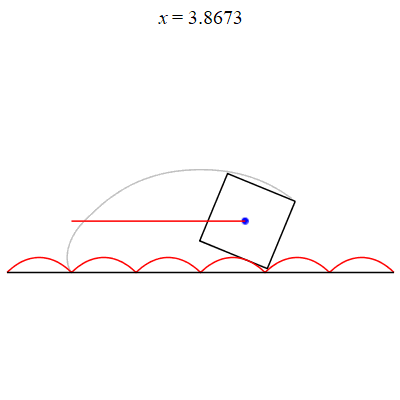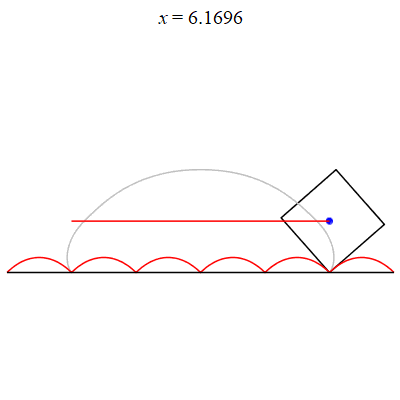
On an inverted catenary curve, the center of a square wheel can move horizontally!
 |
This problem can easily be analysed with Calc II and some trigonometry! But Maple makes it come alive! |

|
dr bob on the small tricycle |
 |
dr bob on the large tricycle |
This circular 3d implementation of this single variable calculus problem scales up each circular catenary curve by the distance from the center of the disk, making the problem a multivariable calculus problem on a surface formed from a family of concentric circular catenoid curves of increasing radius.
In this circular configuration, the 3 wheels are of increasing side length so that as they rotate the square wheels fit exactly between the roughly 36 "nodes" joining the successive catenary segments (tangential cross-sections). The solid red curves trace out the center front wheel paths while the broken red curves trace out the rear wheel paths. Differential equations provide the catenary curve as the workhorse of this mathematical idea, while this circular 3d implementation moves the problem into multivariable calculus. The mathematics of truly interesting problems is "cross-disciplinary" in terms of the areas of mathematics which come together in explaining them.
bob discovered this problem when it was the topic of a problem on the Italian scientific high school graduation exam in 2017, which covers Calc 1 and 2 topics together in challenging problems. This one uses both integration (arclength) and differentiation (slope) together with trigonometry (right triangles). The MOMA visit was in 2020.