 figure
explanation
figure
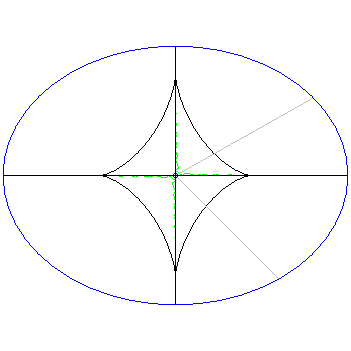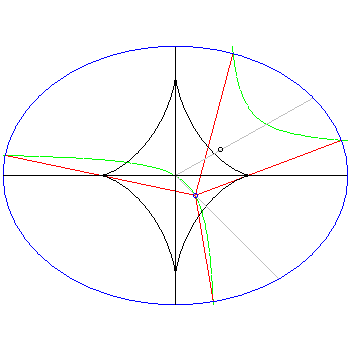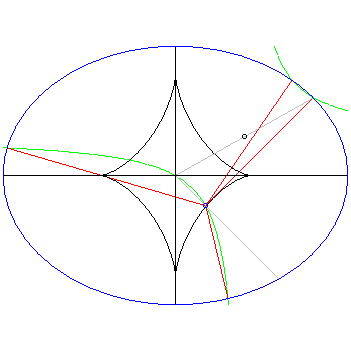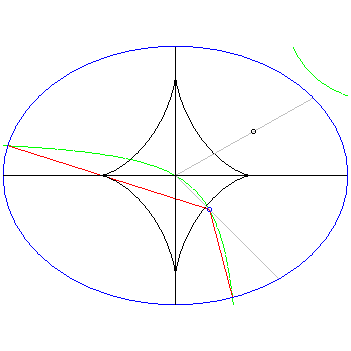
explanation22 centuries ago, with not even the appropriate mathematical symbols or language to express quadratic relationships simply, Apollonius explored the geometry of the conic sections in great detail. In particular he devoted one of his eight volumes on this topic entirely to the distance problem: given a point in the plane, what points on the conic section correspond to the local extrema of the distance between that point and a point on the conic section. This in turn is equivalent to studying how many normals can be drawn to the conic from a given point on the plane. We examine the situation for ellipses.
Armed with a computer algebra system (MAPLE) and the ideas of college level calculus, for which the distance problem is an interesting max/min problem in one independent variable once the ellipse is parametrized, we stumbled upon the geometry that Apollonius had explored in a much more laborious way, showing first the power of our modern mathematical language that we take for granted and second the power that computer algebra systems can wield in playing with mathematical ideas.
The following is a 120K MAPLE worksheet that explores this geometry for an ellipse by defining graphical procedures which allow us to see for ourselves how things work. It uses the tools of the MAPLE VecCalc package which is available at http://www.mapleapps.com but can be obtained from its authors, specialized to plane curves by hand. When executed, the worksheet reaches a size of about 3MEG. These ideas could be used to explore similar questions for other conic sections or other curves.