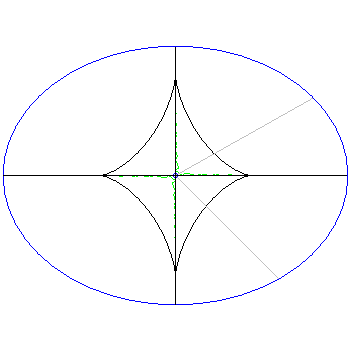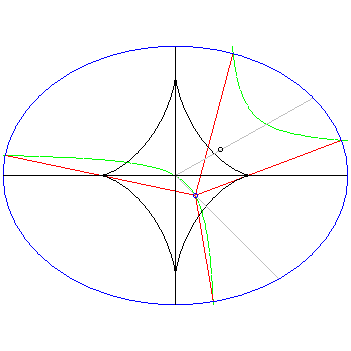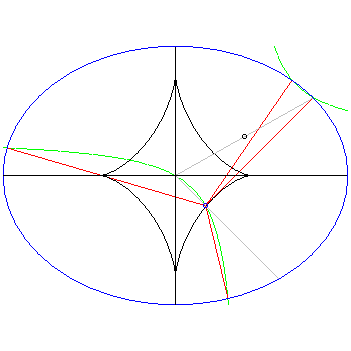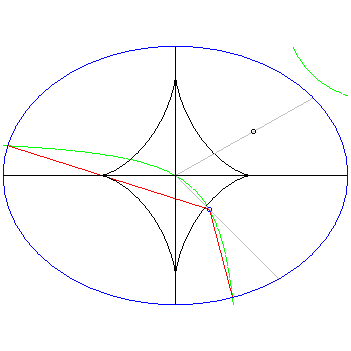
A fixed ellipse [blue] is shown with its evolute [black] (the locus of centers of the osculating circles of all points on the ellipse, here a curve called an astroid). For a point [blue] which moves down and to the right from the center of the ellipse along a straight line [grey], initially 4 normals [red] to the ellipse pass through it, emanating from the points on the ellipse where the moving hyperbola of Apollonius intersects the ellipse. In turn the center of the hyperbola [black] moves up and to the right from the center along a straight line [grey] until one branch becomes tangent to the ellipse and only 3 normals pass through the given point, itself located on the evolute, and then as the point passes out of the evolute the second branch of the hyperbola moves outside the ellipse. The animation is purposely slowed down as the given point passes through the evolute to show more detail of the coalescing normals.
