MAT5600 08S homework and daily class log

Your homework will appear here each day as it is assigned, with occasional links to some MAPLE worksheets when helpful to illustrate some points where technology can be useful. [There are 42 class days in the semester, numbered consecutively below and labeled by the (first initial of the) day of the week. Monday, January 14 thru May ?.]It is your responsibility to check it here. You are responsible for any hyperlinked material here as well as requesting any handouts or returned tests or quizzes from classes you missed. Homework is understood to be done by the next class meeting (unless that class is a test, in which case the homework is due the following class meeting).

W: GETTING STARTED STUFF. By Friday, January 18, e-mail me [robert.jantzen@villanova.edu] from your OFFICIAL Villanova e-mail account (which identifies you with your full name) with the subject heading "[MAT5600]", telling about your last math courses, your comfort level with graphing calculators (can you do symbolic derivatives and integrals on your graphing calculator if not in Maple?) and computers and math itself, how much experience you have with MAPLE (and Mathcad if appropriate) so far, why you chose your major, etc.
[In ALL email to me, include the string "mat5600" somewhere in the subject heading if you want me to read it. I filter my email.]

In class:
1) log on to your computer and open Internet Explorer. (IE allows you to open Maple files linked to web pages automatically if MAPLE is already open or if it is available through the Start Menu Program listing under Math Applications, otherwise use the "File Menu" "Open URL" feature to open a worksheet on the web.)
2) log on to the Villanova home page in Internet Explorer (click on the upper right "login" icon and use your standard VU email username and password) and check out our My Courses classroom site, and visit the link to my course homepage from it
[ http://www.homepage.villanova.edu/robert.jantzen/courses/mat5600/ ],
3) Open Maple 11 Standard (red not yellow icon) from the Start Menu Program listing under Math Applications
[or click on this maple file link: oneforms.mw]
4) bob will quickly show you the computer environment supporting our class. And chat up a bit the course.

Afterclass:
5) log on to MyWebCT and look at the Grade book: you will find all your Test and Maple grades here during the semester.
[This is the only part of WebCT we will use this semester.]
Check out the on-line links describing aspects of the course (no need yet to look at the MAPLE stuff). Fill out your paper schedule form (get a copy in class to fill out or print it out back-to-back earlier to fill out in advance and bring to your first class already done) to return in class Wednesday.
[You can drop by my office St Aug 370 (third floor, Mendel side, by side stairwell) to talk with me about the course if you wish and to see where you can find me in the future when you need to.]
6) Make sure you can access and open Maple 11 Standard in citrixweb on your laptop. If you have any trouble, email me with an explanation of the errors. If I receive no email, it means that you were successful.
You are expected to be able to use Maple on your laptop or in class when needed.

7) Read computer classroom etiquette. Then read the first paper handout: algebra/calc background sheet.

Actual HW: Read the preface and introduction to bob's book. And the open the worksheet oneforms.mw and read that (Use the "File Menu" "Open URL" option of Maple on your laptop). Also find your old calculus book and read the section on hyperbolic functions (Stewart 5e, section 3.9).

Citrixweb is down Tuesday evening, so here is the HTML export of the worksheet which does not allow you to rotate the 3D plots but you can do that later.

Brief talk about index positioning on vectors and linear function coefficients and the dot product and linearity.
W: return your schedule forms at the beginning of class [did you use the 3 letter dorm abbreviations?];
Read pp 105-109 Flow lines of vector fields from bob's book. [Use the View Menu, Go To, Page in Adobe.] Do the exercise there. [Some recalling of details if you get stuck, and a new review of hyperbolic functions (appendix C of bob's book) and the hyperbolic geometry they determine,] And for a field plot or directionfield, see this easily changed example.]

Following up the HW reading, bob reviewed linear functions in the plane and the geometry of addition of covectors and then rambled a bit about the contents of the reading for the next day on DEwLinAlg topic of solving a linear homogeneous system constant coefficient DEs, pushing it past the eigenvector technique to show how the result is just the matrix exponential, using rotations in the plane as an explicit example without doing the eigenvector details. Hopefully by reading and working the HW problem (which is basically solved in the PDF link), it will become clearer.
F: Ask questions...
Read sections 1.1, 1.2 of bob's book on a vector space and its dual space. Do the one problem in section 1.2.1. Also I will add a final part to the hyperbolic appendix with some problems for you to do (almost done except for two illustrations).

WEEK 2[-1]:
W: If our discussion in class allows, we move on to read section 1.3 on the linear transformations of a vector space and tensors which builds on 1.2 (finish that section by doing Exercise 1.2.2). [For the direction field for the hyperbolas see resources/maple/fieldplotex2.mw.
Note Wikipedia has interesting entries for many of the terms we are encountering, like the dual space. An inner product is called a quadratic form in the old language (more precisely it determines an associated symmetric form which corresponds to the inner product) while a linear (homogeneous) function is called a linear form in the old language, so sometimes I will refer to a covector as a 1-form, for first degree form, i.e., linear form.
F: Exercise 1.2.2 [by hand, maple]; course info sheet, bob's cell; go back and consider new exercise 1.3.1 on the quadruple scalar product;
read 1.4 on changing the basis and dual basis.

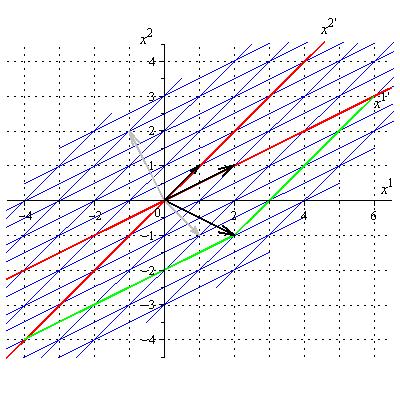
Week 3[-1]:
M: start 1.5 on inner products. We will take a few days on this one. Do the problem on the Gram-Schmidt orthogonalization procedure below.
An inner product is just a symmetric bilinear function of a pair of vectors from a vector space and hence can be identified with a symmetric matrix with respect to a given basis. If it is nondegenerate (i.e., nonzero determinant) then a simple orthogonalization procedure ([Wiki], called Gram-Schmidt [Wiki: see the explicitly worked 2-dimensional example] can be used to take any ordered basis and create from it an orthonormal basis of mutually orthogonal unit vectors. This automatically not only diagonalizes the matrix of components, but results in diagonal values which have absolute value 1. The number of negative and positive signs is always the same because it is uniquely associated with the signs of the eigenvalues of the matrix. A positive-definite (negative-definite) inner product has all positive (negative) signs, an indefinite one has a mix of signs. We usually deal only with the positive-definite dot inner product on Rⁿ. Apply Gram-Schmidt to the columns of the upper triangular matrix whose entries are all 1s: G = <<1,0,0>|<1,1>|<1,1,1>> in the order from left to right or from right to left (you get two different results). This is now problem 1.5.3, which has more parts to it. and 1.5.4. Not to mention the already present 1.5.1-2.
W: Continue reading 1.5 on inner products. Work on the problems.
F: Finish up 1.5, just reading but not doing the long final Exercise 1.5.8. The geometric interpretation of an inner product is cute but not necessary so don't waste too much time on that section. In class we discussed the Gram-Schmidt diagonalization problem, and the second derivative problem with the elliptic paraboloid.
Begin reading 2.1 and 2.2 through exercise 2.2.2.

WEEK 4[-1]:
M: We discussed the tensor transformation law problem from 1.4, and then based on the area of a parallelogram in the plane and the volume of a parallelepiped in space, motivated the information contained in the determinant function thought of as a tensor on Rⁿ accepting n vector inputs. For a set of n vectors, it contains 1) the volume of the n-parallelepiped they form [absolute value], 2) orientation (ordering) information [sign]. Evaluating the determinant on p less than n vectors leaving some slots free contains information about those p vectors: 1) volume of the p-parallelepiped they form, 2) "inner orientation" (ordering), 3) orientation (direction), namely how the p-parallelepiped is directed in the n-space. The permutation group is behind the definition of the determinant. We need some better notation to handle it as a tensor with our index conventions.
Finish reading 2.1,2.2 and do the problems, and when ready move on to 2.3. [I broke off part of 2.2 to become the new 2.3].
W: We will discuss the elliptic paraboloid curvature problem 1.5.4 last two parts, and the problems from 2.2, 2.3.
Please stop by to find my office in the next two weeks. Say hi.
Read the short section 2.4 and move on to the review so far, chapter 3. Make sure you did or can do all problems so far.
F: What did we do today?

WEEK 5[-1]:
M: bob started by discussing the 3-dimensional vector space of 3x3 antisymmetric matrices, introducing a natural basis of this space and then of its dual space, and the identity tensor etc, and then showed how the 2 pair indexed Kronecker delta was really just that identity tensor expressed in terms of pairs of indices with respect to the original vector space R^3 above which the matrices can be interpreted as the components of second rank tensors. with the example of projecting a vector in R^3 into its piece along a plane subspace and its piece orthogonal to the plane along the line subspace by subtracting away the projection in the orthogonal direction. The projection operation acts as the identity on each subspace, since projecting something already in a subspace does nothing. Working instead with the 9-dimensional vector space of all 3x3 matrices, we can project out the 3-dimensional subspace of antisymmetric matrices and the 6-dimensional subspace of symmetric matrices in a similar way. Again from this point of view the 2 pair indexed Kronecker delta just projects out the antisymmetric part and then acts as the identity on tensors which are already antisymmetric. The complication of the Kronecker deltas is that the distinct groups of indices function as the labels for the independent tensors in each space, so we must use groups of indices in order to reproduce things which are simple in terms of an ordered basis of each separate tensor space labeled from 1 to the dimension of each space. Try to start reading chapter 4.
W: Read 4.1 and do the exercises. COME for OFFICE VISIT PLEASE. SNOW DAY, to be made up later in semester?

Did we miss Valentine's Day: ?
F: In class we discussed the wedge product easily, bypassing the component formulas. Then showed how it leads naturally to the unit n-form η ("eta") which hardwires the determinant, and then the duality operation.
For the weekend Read 4.2 and do the exercises.

WEEK 6[-1]:
M: bob discusses how one determines subspaces of Rⁿ corresponding to the newly added subsection of 4.2.
W: Take Home Test 1 thru Part 1 out:
Problems 1.6.4 (second derivative test extended slightly), 4.2.16 (2 vectors in R⁴), 4.2.17 (games in R²). [The last two problem numbers changed recently from 4.2.14, 4.2.15 by the addition of two earlier problems.]
Do your best to organize your work well documenting it like a report so one does not need to refer back to the problem wording to follow what you are doing, i.e., not just to get the answers. Work independently please, and come to me if you are confused.

PART 2 begins. Read 5.1. Everybody must come see me before break to get a midterm grade...
F: SNOW DAY.

WEEK 7[-1]:
M: It is about time we looked at Maple together. cmdlist3.mw; tangentvectors.mw;
Maple tips and hints [Why MAPLE?][VU MAPLE FAQ][Maple hype][training videos]
W: We start with questions about 5.1. Read 5.2.
F: Leap Day!
Reread 5.3, look at the new exercises added to it. Test1? Midterm grade S?

Spring Break. enjoy and be safe.

WEEK 8[-1]:
M: 5.4 Read. Try problems 5.4.1-4.
W: 5.5 non-Cartesian coordinates: polar coordinates in the plane as an example.
Midterm grades due noon.
F: Read 5.6 – 5.8 cylindrical coordinates, spherical coordinates, and their frames.
Today 3/14 is π-day! [and Einstein's birthday]

WEEK 9[-1]:
M: The covariant derivative is introduced by transformation from cartesian coords: Read 5.9 and begin chapter 6.
W: The components of the covariant derivative are expressed in terms of the metric. Read through chapter 6 for next Wednesday.

Easter Recess:

WEEK 10[-2]:
W: Chapter 6
F: Chapter 6

WEEK 11[-2]:
M: Rob GP-B talk
W: 6.6-6.7 discussion, noncoordinate frame components of covariant derivative, handwaving about 6.3 covariant diff and linear group
F: Read 7.1-7.2.

WEEK 12[-2]:
M: Read 7.3-7.4.
W: Start chapter 8. read 8.1.
F: Read 8.2-8.3, in class: 9.1 calculation of curvature. read 9.1.

WEEK 13[-2]:
M: interpretation of curvature 9.3 in class, read 9.
W: read chapter 10 (short) on extrinsic curvature.
F: now finish chapter 8,
one problem for the take home final is problem 8.6.3 at the end of chapter 8 on torus geodesics [use torus_geodesics.mw for experimenting with geodesics],
CHANGE in wording of part c) which made no sense as worded;
the second problem is problem 10.4.2 at the end of 10.4 on the saddle surface extrinsic curvature [use tensor_package_test.mw for the evaluation of the curvature of the saddle surface (Maple gives the opposite sign because of a different convention); just edit one of the 2-dimensional metric examples and re-execute that section.],
CHANGE in wording of part d) to clarify it.
black hole orbits are easy too!

WEEK 14[-2]:
M: Finish reading chapter 10 on extrinsic curvature.
W: Begin final chapter 11, read at least 11.1-11.3.
F: Read 11.4-6.

WEEK 14:
M: Read 11.7-8 on exterior derivative and metric, induced orientation.
perhaps the handwritten examples are slightly more readable until I finish editing the typeset version

dg12.pdf Induced orientation etc through end of chapter 11
T[F]: Read 11.9-10 .
W[M]:

bob's book in progress [bob's maple worksheets] [citrixweb]

Weeks 3 thru 4: come by and find me in my office, tell me how things are going. This is a required visit. Only takes 5 minutes or less.

FINAL EXAM: Probably will be a take home exam. At least two take home tests during the semester. We'll play it by ear.

28-apr-2008 [course homepage]