Sometimes nature is too beautiful for words. This is one of the reasons why mathematicians have been so useful over the centuries. While the origins of mathematics lie in mundane processes like counting, the field has been steadily expanding since that time. One of the most significant changes resulting from the growth of mathematics is that it has become less and less focused on the practical and more and more focused on the theoretical. This has been a very slow process, as mathematics is still somewhere between the two extremes. Regardless, this glacier-like revolution has spawned a lot of beautiful mathematics that might not have otherwise come about. One such invention is the study of curvature.
Many curves in the plane and in space are simply beautiful. Since words cannot do them justice, mathematicians have developed several ways of describing them. The most common method of describing a curve is to give its parameterization. Another way, however, is to say how much the curve "bends" at each point. This measure of bending is known by the technical word "curvature". It may surprise the reader that curvature is all that is needed to define a curve (up to rigid motions). For example, a curve that has constant curvature must be part or all of a circle (for these are the only curves that have the same amount of bending at every point). The study of this twisting property of curves goes back to ancient times, but few of its goals were realized until the invention of the calculus in the seventeenth century. Throughout the history of mathematics, the analysis of the curvature of curves has been a prime illustration of the beauty of mathematics and an indicator of its progress.
The history of geometry in general has three very distinct stages: ancient geometry (Ancient Greeks), analytic geometry (Fermat and Descartes in the seventeenth century), and finally differential geometry (modern times) (Gamkrelidze 14). All along, curvature has held the attention of many great mathematicians. In Ancient Greece, for instance, there was a clear distinction between the curvatures of the classical Greek curves, the line and the circle. Simply, the distinction was that lines don’t bend, and circles bend the same at every point (McCleary 66). According to Proclus’ history of geometry, Aristotle expanded upon these notions, declaring that there were three kinds of loci: straight, circular, and mixed (Coolidge 375). These monumental notions were the germination of what eventually became the study of curvature. As stated in the Encyclopedia of Mathematical Sciences, the main result in the development of geometry from Ancient Greece to the present is the move from "archaic synthetic form into modern differential form" (Gamkrelidze 22). The process began with Aristotle and his contemporaries, but generalization and rigorization of this would come centuries later.
The next in the line of landmark geometers is Apollonius of Perga, who lived in the third century B.C. Among his more significant findings was that at each point of a conic section there is exactly one normal line (Coolidge 376). This fact is one that would show its relevance to the study of curvature at a much later time. More importantly, in the fifth book of his Conic Sections are found the "germs of the subject of evolutes and centers of osculation", subjects intimately related to curvature (Cajori 49). According to the mathematical historian D.T. Whiteside, Apollonius applied methods for finding the radius of curvature which were amazingly similar to the methods used by Huygens and Newton two thousand years later (Whiteside 175). Unfortunately, neither Apollonius nor his contemporaries could take their geometrical ideas beyond the limits of their meager methods (such as exhaustion). Regardless, the work of these mathematicians was indispensable in the progess towards the study of curvature.
As the first one and a half millennia of the Common Era produced few helpful methods in the area of curvature-related geometry, there were few advances in the field. Finally, in the fourteenth century, Nicole Oresme made a relevant contribution. Oresme is generally esteemed to be the fist person to draw a graph, and his work is viewed by some scholars to be an early attempt at coordinate geometry (Struik 1986 133). He also seems to be the first writer to hint at a definition of curvature. In fact he assumed the existence of a measure of twist called "curvitas" (Coolidge 376). He also indicated his awareness that, as in Figure 1, if two curves have the same tangent at a point and one is "inside" the other, then it has greater curvature (Coolidge 376). As was obvious to Oresme, it bends more. Additionally, Oresme remarked that the curvature of a circle is "uniformus" (Coolidge 376). He went on to propose that the curvature of a circle is proportional to the multiplicative inverse of its radius (Coolidge 376). Part of the importance of Oresme’s work is that it helped rekindle the fire that became the mathematicians’ drive to find the curvature of a general curve.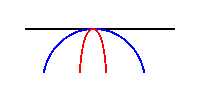
Figure 1
Almost three centuries later, Johannes Kepler (1571-1630) made indirect contributions to the theory of curvature. His first donation was his generalization of the Problem of Alhazin). Kepler generalized Alhazin’s solution and discovered a method for finding the image of a brilliant point when reflected off of a general curve. Part of Kepler’s genius was to approximate the general curve with a circle at the point of reflection, thus reducing the problem to that of Alhazin (Coolidge 377). In later times, this approximating circle would come to be known as the "circle of curvature" of a curve at a point; for the radius of the circle is inversely proportional to how much the curve bends at the point. Kepler’s work was instrumental in the development of curvature, for he seems to be the first to actually develop methods for investigating the degree of twisting in a curve.
Another great advance in man’s pursuit of curvature was taken by the first analytic geometers. Most notably, this includes Pierre de Fermat and Rene Descartes. Their most important contribution was to describe general geometric curves with algebraic equations. This was obviously essential in order for curves to be treated by calculus (or for calculus to be invented, for that matter). Unfortunately, however, these mathematicians were still lacking one major ingredient useful in the analysis of curves and circles--pi. This was a major hindrance in the geometrical work of the time. Descartes lamented, "the ratios between straight and curved lines are not known, and I believe cannot be discovered by human minds, and therefore no conclusion based upon such ratios can be accepted as rigorous and exact" (Katz 403). Thus, the growth of analytic geometry in the seventeenth century was stunted, and the explicit invention of curvature was preempted.
In 1673, a mathematician named Christiaan Huygens published the influential book Horologium oscillatorium sive de motu pendulorum ad horologia aptato demonstrationes geometrica. Most significantly, this work deals with evolutes and involutes of curves. He describes a very specific method for finding the "involute" of a curve. As seen in the accompanying demo, in order to find the involute of a curve A, one should wrap a string tightly against A, on its convex side. Then, keeping one end of the string fixed, the other end is pulled away from the curve. If the string is kept taut, then the moving end of the string will trace out a curve, B. B is called the involute of A, and A is called the evolute of B (see demo)(Coolidge 377). What is important is that each step of the way, the string is tangent to the evolute and perpendicular to the involute. Huygens "attempt[ed]" to define the radius of curvature of the involute as the distance between the points of contact between the involute with the string and evolute with the string (Coolidge 377). This working definition of curvature is exactly what the curvature of an involute would come to be defined as. Huygens even specifically stated that the locus of the "centers of curves", one on each normal, is the evolute of a curve (Kline 556). This definition has also remained unchanged ever since. However, Huygens’ method required the evolute to be given in advance. This did not help if one wanted to find the radius of curvature of an arbitrary curve. In order to find what was happening in a "really really small" portion of a general curve, calculus would be needed. Calculus had already been invented by the time Huygens published Horologium oscillatorium, but Huygens was not yet cognizant of its methods. Therefore, Huygens had only a general method and could not find an exact solution to the problem of curvature.
Figure 2
One of Huygens’ most impressive accomplishments in Horologium oscillatorium was his work with the cycloid. Huygens showed geometrically that the evolute of the left half of the lower cycloid is the right half of the upper cycloid (Figure 2). He did this using "synthetic and infinitesimal ideas" (McCleary 78). This, combined with the fact that the cycloid is a tautochrone, led to Huygens’ genius invention, the cycloidal pendulum. The idea is that if a pendulum (bob on a string) is swung between the arches of a cycloid (see demo), then the bob of the pendulum will trace out the involute of a cycloid--a cycloid. Since the cycloid is a tautochrone, the pendulum will retain its period even as its amplitude decreases in time. Under ideal conditions (no friction or air resistance), this would make for a perfect time-keeper. Huygens' Pendulum is a very practical application of curvature, and it would prove to serve as inspiration for further investigation of curvature by later mathematicians.
Finally, in the late seventeenth century, the Calculus was invented and turned the House of Math into a metropolis. More specifically, Calculus’ methods of infinitesimals and limits were the perfect tools for the problem of curvature. (In fact, Huygens had already tried to give a description of curvature using limit-like ideas.) Because most curves have a different degree of bending at every point, mathematicians needed a method to look at an "infinitely small" part of a curve in order to say what was happening at a particular point. Calculus became this prescribed method.
Of the two "co-discoverers" of the calculus, Sir Isaac Newton and Gottfried Wilhelm Leibniz, Newton was the one who did more extensive (and more accurate) work with curvature. He seemed to be attracted to this subject primarily for its beauty. In Problem 5 of his Methods of series and fluxions (To find the curvature of any curve at a given point), he begins, "The problem has the mark of exceptional elegance and of being pre-eminently useful in the science of curves" (Whiteside 151). Newton started to investigate the problem of curvature by listing its most elementary properties:
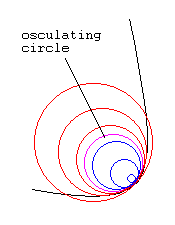Figure 3Newton’s definition of center of curvature is significant because it is the first place in his work with curvature where he uses the concept of infinitesimals. About the center of curvature, he states, "It is the meet of normals at indefinitely small distances from [the point in question] on its either side" (see demo) (Whiteside 153). Newton used this very method to at long last find an equation for the radius of curvature. By finding the intersection of the normal at the point in question and an infinitely close normal, Newton derived the following formula for curvature:
Newton derived a similar equation for use with polar coordinates (Kline 364).
One of Newton’s observations regarding his equation for curvature was that it will yield an undefined number at points of inflection (Coolidge 378). As he noted, curves behave like a straight line near a point of inflection (they don’t bend either way), and since the radius of curvature of a straight line is infinite, the radius of curvature at these points is infinite. Newton used the term "point of straightness" to describe inflection points, and gave the example ax3 = y4 (Figure 4) to illustrate his point.
Figure 4
Newton also set down that the points of greatest or least flexure (bending) of a curve can be found by setting the fluxion of the radius of curvature equal to zero (Whiteside 181). This is exactly his method of finding maxima and minima applied to radii of curvature. In modern differential geometry texts, such points are called "vertices". Also, Newton remarked that cusps can be found by setting the radius of curvature itself equal to zero (Whiteside 181).
Newton also calculated the formula for radius of curvature for several curves, including the cycloid and the Archimedan spiral (Kline 556). In doing so, he reproduced Huygens’ result that the "locus of centre of curvature" (evolute) of a cycloid is a cycloid. Of course, Newton did it with his own analytic methods as opposed to Huygens’ geometrical means. Furthermore, Newton re-invented Huygens’ cycloidal pendulum (Whiteside 163). It is unclear whether or not Newton made these discoveries himself or was made aware of them though other mathematicians. What is clear is that Newton’s methods were his own. The ease with which he was able to derive these results is what is most impressive.
Other mathematicians of Newton’s time also worked on the problem of curvature. However, none were as prolific, and none were as successful. For example, Leibniz (who also claimed to have invented the calculus), was the one who gave the circle of curvature the name which has stuck ever since--the "osculating circle" (Kline 378). One of the reasons why Leibniz’s work with curvature is not given very much recognition is because of a very fundamental error he made. In one of his works regarding curvature, Leibniz made the claim that an osculating circle has a four-point contact with a curve near the point for which the circle is drawn (Coolidge 377). James Bernoulli very promptly pointed this out this mistake (Coolidge 377). Incidentally, James and his brother, John Bernoulli, gave their own formula for curvature in 1691. James called it the "golden theorem" (Kline 382). This theorem stated that the radius of curvature of a curve was equal to two equivalent ratios:
dx ds : d dy = dy ds : d dx
James also gave this result in polar coordinates.
In the following century, many Calculus text books were written, and many dealt with the subject of curvature. Marquis de L’Hopital included Newton’s formula for the radius of curvature in his Analyse (Katz 446). In 1731, Alexis-Claude Clairaut (1713-1765) became the first geometer to publish on "curves of double curvature" (Kline 557). In modern language, such curve are simply space curves (curves in three-dimensional space). Clairaut’s "new" curvature, which he named "torsion" was a measure of how quickly a space curve pulls away from the plane of its osculating circle at a point (Kline 559). In order to study such curves, Clairaut borrowed one of Descartes’ methods and projected his space curves onto two perpendicular planes, then treating these projections as regular plane curves (Kline 557). Clairaut’s work was significant, because it paved the way for later geometers, such as Gauss, to study the curvature of surfaces, which also bend in two directions.
Thomas Simpson, in his book on the method of fluxions, also dealt with the subject of curvature. In Section V (The Use of Fluxions in Determining the Radii of Curvature, and the Evolute of Curves), he described the string-construction of evolutes which was developed by Huygens. Simpson also used an interesting description of curvature. He stated that the degree of curvature is equivalent to the second fluxion of the curve, and this is a measure of "deflection from [the] tangent" (Simpson 53). This is an important observation because it directly links the first and second fluxions of a curve.
Leonhard Euler is the mathematician responsible for the important theorem that the magnitude of curvature equals the magnitude of the second derivative of a parameterization at a point (McCleary 67). As parameterized curves would eventually become central to differential geometry, this was a monumental discovery. In 1774, Euler made more revolutionary statements about curvature. Most importantly, he devised a new way of defining curvature. To each tangent vector of a curve he assigned a point on the unit circle which corresponds to the direction of that tangent vector (see demo). Then, he defined curvature as ds’/ds, the change in angle of the tangent divided by the change in arc length (in an infinitely small locale) (see Figure 5) (Kline 559).. On an intuitive level, one can see that a large change of angle in a short distance will produce a large curvature, as Euler’s equation indicates. In addition Euler produced an analytical expression for the radius of curvature: 
(Kline 559). Even though Euler was describing concepts that were a century old, it seemed like he was inventing new concepts, for his methods of studying curvature were very innovative.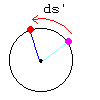
Figure 5
In 1826, Augustin-Louis Cauchy made a significant improvement to differential geometry. In his Lecons sur les applications du calcul infinitesimal a la geometrie, he cast off the idea of constant infinitesimals (Kline 560). He rightly regarded infinitesimals as quantities which were approaching zero. He also "straightened out the confusion" between differentials and increments (Kline 560). He noted that ds2 = dx2 + dy2 + dz2 should be more properly written as (ds/dt)2 = (dx/dt)2 + (dy/dt)2 + (dz/dt)2 (Kline 560). These were important distinctions not only for differential geometry, but for calculus in general as well.
Thomas Hill wrote another text on curvature, called An Elementary Treatise On Curvature. Much of this work is regurgitation of his predecessors’ findings. However, Simpson does offer something which was a fairly novel finding, whether of not he originated the idea. In the chapter concerning the classification of curves he states, "An equation between the radius of curvature . . . and the angle it makes with a given direction, implies all the conditions of the form of the curve, though not of its position" (Hill 15). Eventually, this (slightly modified) would come to be known as the Fundamental Theorem of the Local Theory of Plane Curves. In modern differential geometry textbooks, this theorem is not attributed to a specific mathematician, so it just seems to have been a "product of the times". Hill can be thought of as a representative of the mid-nineteenth century, as his textbook encompasses most of the differential geometry and applications of the time.
Karl Friedrich Gauss brought differential geometry to a whole new level. He is known primarily for his work on the theory of surfaces. He produced a formula for curvature which was very similar to Euler’s, and from this he derived the following profound analogy: arc : amplitude : curvature :: time : motion : velocity (Gauss 83). In order to understand this, one should think of a point moving along a curve with uniform velocity with respect to arc length. Then curvature is a measure of the amplitude of the curve. Gauss realized an ingenious method for measuring the curvature of a two-dimensional surface in three-dimensional space. The so-called Gaussian curvature of a surface at a point is the product of the greatest and least curvatures of all curves passing though that point in the surface. Most of Gauss’ findings deal with complicated properties of surfaces and are beyond the scope of an introductory exploration of curvature. Gauss did add a new dimension to the study of curvature and will always hold a place in its history.
Mathematical treatment of curvature underwent a drastic metamorphosis over the history of the problem. Differential geometry started with vague definitions and simple concepts and developed into the well-oiled machine that it is today. Clearly, the most dramatic leap came when the Calculus was invented. Differential geometry and curvature were natural applications for the Calculus because they provided words to its music--practical applications (map making, light ray travel, etc...) to the theory. Since then, mathematicians have become more proficient with the concept of infinitesimals--one no longer speaks of "adjacent points" in the same way that Newton did. In any case, this author is certain that the journey has only just begun. Gauss made the leap from curvature of one-dimensional curves to the curvature of two-dimensional surfaces in three-dimensional space. It will not be long before common mathematicians are proficient with the three curvatures of a three-dimensional surface lying in four-dimensional space. As Gauss said, "The subject is still so far from being exhausted" (Katz 693). And so are the mathematicians.
