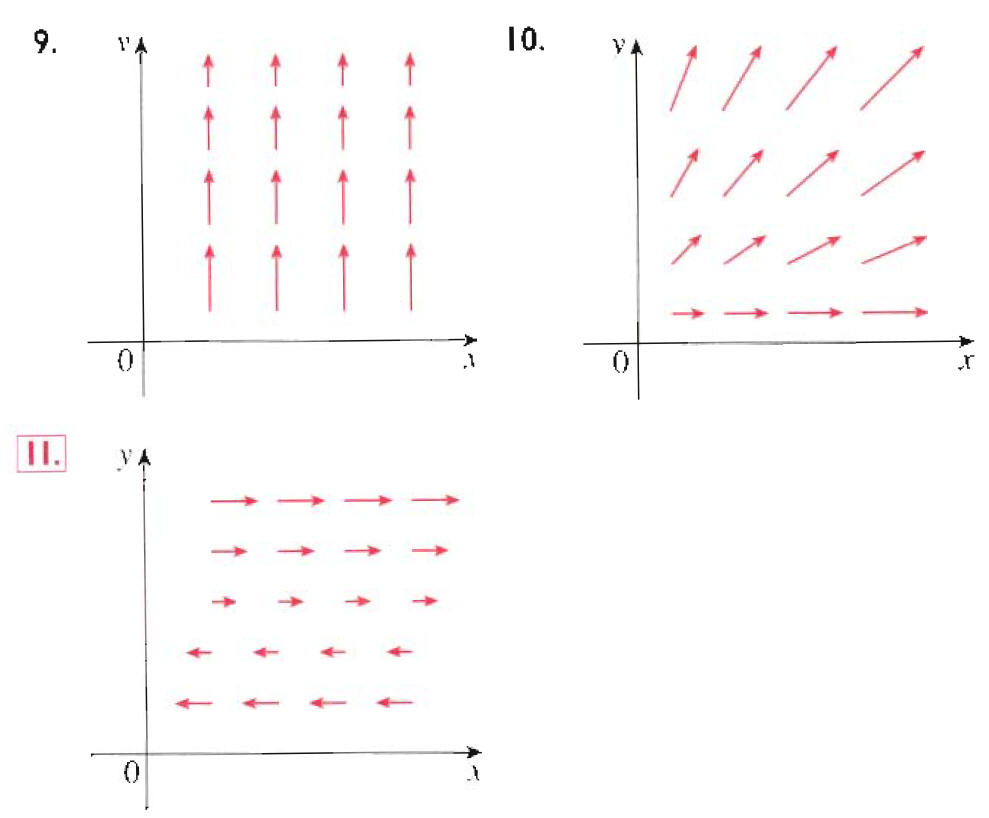
Stewart Calculus 8e. 16.5: 9-11.
In each of these examples we want to use the apparent sign of the derivative of components with respect to the coordinates to infer the sign of the curl or divergence: div(F) = ∂ F1/∂ x + ∂ F2/∂ y and curl(F)3 = ∂ F2/∂ x - ∂ F1/∂ y
a) Is div positive, negative, or zero? Explain.
b) Determine whether curl = 0. If not, in which direction does curl point?
Look at 10. for fixed x, moving up the x component does not change so ∂ F1/∂ y =0, but the y component increases: ∂ F2/∂ y > 0. Repeat for a fixed y, moving to the right and you get one derivative is zero, the other positive. With these two signs alone, you can determine the sign of div and curl.
Similar considerations work for all these vector field plots.

Email bob if you cannot get the correct responses to any of these problems.
These are obvious observations of the various plots. Inserting them into div and curl we can draw our conclusions.
9. F1 = 0, (so ∂ F1/∂ x = 0, ∂ F1/∂ y = 0), ∂ F2/∂ x = 0, ∂ F2/∂ y < 0,
10. ∂ F1/∂ x > 0, ∂ F1/∂ y = 0, ∂ F2/∂ x = 0, ∂ F2/∂ y > 0,
11. ∂ F1/∂ x = 0, ∂ F1/∂ y > 0, F2 = 0, (so ∂ F2/∂ x = 0, ∂ F2/∂ y = 0)
so
9. div F = ∂ F1/∂
x + ∂ F2/∂ y < 0
( curl F)3 = ∂ F2/∂
x - ∂ F1/∂ y = 0
10. div F = ∂ F1/∂
x + ∂ F2/∂ y > 0
( curl F)3 = ∂ F2/∂
x - ∂ F1/∂ y = 0
11. div F = ∂ F1/∂
x + ∂ F2/∂ y = 0
c ( curl F)3 = ∂ F2/∂
x - ∂ F1/∂ y < 0