
Ans.
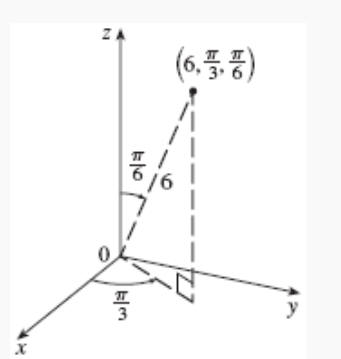
Clearly the 30 degree angle is the angle down from the vertical (phi) and the 60 degree angle is the angle around the z axis (theta).
In the real world outside of calculus textbooks, as used universally in physics, the letters representing cylindrical and spherical coordinates and their ordering is different. WIkiipedia has nice diagrams showing these conventions.
Wiki: cylindrical coords, spherical coords.
Calculus textbooks start from polar coordinates (r,θ) and just add z to get cylindrical coordinates (r,θ,z) and then introduce two new letters for the spherical coordinate radial variable ρ and angle φ down from the vertical (to make matters worse, "phi" has two forms, called "phi" and "varphi"in Maple; in HTML code varphi is used). The authors are afraid students will be confused if confronted with completely new names.
So the calculus cylindrical variables (r,θ,z) become
respectively (ρ,φ,z)
while the calculus spherical variables (ρ,φ,θ) become respectively
(r,θ,φ) in this order, to make the three orthogonal
coordinate directions "right-handed" like the Cartesian coordinates (x,y,z),
namely their unit vector directions satisfy the same cyclical cross-product algebra as the three unit vectors
(i,j,k).
Stewart Calculus 15.8 also states spherical coordinates in the "wrong" order (ρ,θ,φ) in its description while failing to identify what they mean in some exercises. Always IDENTIFY your expessions with the symbols which represent them to the left in an equation: "symbol" = "expression".
Below should read (ρ,θ,φ) = (6,Pi/3,Pi/6).
Stewart Calculus 8e. 15.8.

Ans.

Clearly the 30 degree angle is the angle down from the vertical (phi) and the 60
degree angle is the angle around the z axis (theta).