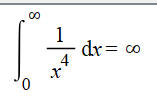
One of the motivations for Einstein's Nobel prize was solving the ultraviolet catastrophe problem in the physics of light and thermodynamics. [wiki] He actually had 5 different things that led to this prize, but not relativity!
Who has not heard of the famous cosmic background radiation at 2.7 degrees Kelvin, a remnant of the Big Bang? No? Well, the radiation has a power spectrum, namely there is more energy in some wavelengths than others, but the classical theory for the so called black body radiation which describes this is described by an inverse fourth power of the wavelength x = λ (lambda) = 2 π/ω (omega) whose total integral is the total amount of power radiated in all wavelengths (ω), which is infinite!
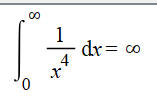
This is improper for two reasons, the explicit infinite limit of integration, and the division by zero at the left endpoint of the interval of integration, which corresponds to short wavelengths (λ << 1) and high frequency (ω >>1). The antiderivative is -1/x^3, which leads to a finite result at infinity, but an infinite result at the origin corresponding to the higher frequencies (shorter wavelength) than light, on the ultraviolet side of the visible spectrum. This can be rewritten as another improper integral for the frequency ω = λ/(2 π), which is the usual way this problem is discussed. In the reciprocal variable the infinity at large values of u is obvious, while it is clearly well behaved at the origin.

This infinite result for the classical black body law was called the "ultraviolet catastrophe", corrected by the quantum mechanics of the photons which make up electromagnetic radiation, which includes light.
Einstein understood how to modify the model to "tame" this latter infinity by actually eliminating the vertical asymptote in the expression for the power spectrum. An Indian physicist later helped Einstein better understand the thermodynamics of this phenomenon, called Bose-Einstein statistics. [wiki] Planck got his name in here too because he came up with the right expression first, but had no idea why it worked. [wiki] No prize for him!
Okay, you have no idea what a black body is, but you do know that the sun delivers energy to the surface of the Earth, measured by the amount of energy per unit time (power) per unit area that the light hits. Most of it is in the visible light wavelengths fortunately for us, because much shorter wavelengths (x-rays, cosmic rays) would kill us! The atmosphere screens out the cosmic rays for us. If we divide the amount of power delivered for each wavelength (power spectrum) by the finite total power in the light, we get a probability distribution (section 8.5!), namely a nonnegative function whose total integral is 1, peaked in the range of visible light. [good plot] It turns out the sun is very close to a black body emitting at 5800 degrees Kelvin. This puts the peak of the sun's output in the safe region!