Each of these courses 1500-1505-2500-2705 have 2 in-class closed book "hour = 55 minute" tests, a third week-long take home open resource test and a closed book in-class 2.5 hour final exam, with about 8 or 9 weekly quizzes during non-test weeks: quiz-test archives [test rules]. Each course has a PDF handout list including some Maple worksheets, but the current complete class daily log and homework page has links to all PDF notes and Maple worksheets.
Why MAPLE? Not just because bob says so!
Maple use in MAT1500-1505-2500-2705 [first
impact message]:
using Maple in Calculus and Differential Equations and Linear Algebra and
resources for instructors
new to Maple
[3
minute video of Maple clickable calculus interface;
15 minute Quick
Start Tutorial Video;
55 minute tutorial on
learning how to use Maple more effectively]
[>>>
Maple
interface for a new user] [Maple
in Calculus etc]
See the Maple Hints and examples page first and the VU Maple FAQ for how to access Maple and deal with its idiosyncrasies. These are meant for instructors who want to dive deep into Maple.
See also:
mplweb.htm calculus worksheets [moved to my own website, links to fix, but see above]
../maple/index.htm many Maple examples accumulated over decades
http://www34.homepage.villanova.edu/robert.jantzen/home.html#MAPLEfiles
more links
Maple's Explore command takes math to the next level by making it interactive
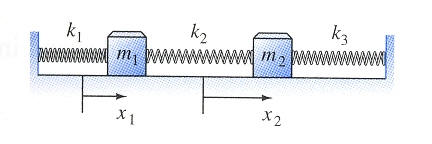
Here is a tease illustrating a force driven periodic undamped 2 mass 3 spring coupled mass spring system

shown in the left diagram below with the two small round masses
oscillating about their equilibrium positions on the vertical axis. These
oscillations are simultaenously being plotted versus time on the horizontal
axis.. The right diagram decomposes those displacements
plotted as a system point in the plane of the two displacements x1 and x2 into the
homogeneous free motion component (blue), the response component (green), and
the total motion (red) (displacement plane on right):
 .
.
A natural extension of this example explores the reaction of a multistory building to horizontal earthquake vibrations. These are the building profiles for the 7 natural modes of vibration of a 7 story building (exaggerated of course, but with correct relative frequencies).
 |
 |
These rely on eigenvalues and eigenvectors. See bob's graphical detemination of eigenvalues and eigenvectors in the plane.
Here is a multivariable calculus tease: a point traces out uniformly a circle in a vertical plane which is itself rotating about the vertical axis. This is a toy model of the GP-B satellite experiment to test Einstein's test of general relativity. [For explanation, see this web page.]

The square wheel problem [statement to challenge math problem solver (pdf), Maple solution and graphics] analyzes a structure anchored in the Serret-Frenet TNB frame of a plane curve (Calc 3!), although one does not need to introduce this language to solve the problem, which only requires single variable calculus. [dr bob visits the Museum of Math square wheel tricycle ride!]

Cavatappo 2.0: geodesics on a corkscrew symmetric helical tube surface. Differential geometry studies the geometry of surfaces etc.

Multivariable integration is not about finding antiderivatives to evaluate definite integrals, it is really about understanding relationships among variables in 2 or 3 dimensions enough to set up limits of integration: iterating a multiple integral. One is really parametrizing the points in such regions as successive intervals in orthogonal coordinates. For example, a double integral [mw, mw] over the region "shaded" by the equally spaced radial linear cross-sections in the second figure below is imagined as an integral over a typical radial linear first figure shows a Cartesian iteration of an integral over an ellipse.
A triple integral [mw] is a sequence of 1d integrations along successive coordinate lines. Here below in the last diagram one integrates first along the vertical z-direction (innermost integral), then this linear cross-section is swept across a vertical plane cross-section in the y-direction (inner double integral), and this finally is swept across the solid region in the final x-coordinate direction (final integral), each time along an orthogonal direction. Once the innermost integral is done, the integral reduces to a double integral on the projection of the solid region down to the plane of the two remaining coordinates, and finally once the next integration is done, it projects down to the final coordinate x-axis for the last integration.



and illustrating medicinal dosing geometric series applications in MAT1505:
